Teknik Integral Parsial
Teknik integral parsial merupakan salah satu teknik pengintegralan yang digunakan ketika integran tidak dapat diintegralkan hanya dengan definisi integral (antiturunan). Teknik integral parsial didasarkan pada pengintegralan turunan hasil kali dua fungsi. Coba perhatikan bagaimana rumus integral parsial diturunkan dari rumus turunan hasil kali dua fungsi sebagai berikut.
Jika y=U(x)V(x) atau kita singkat saja menjadi y=UV maka turunannya adalah sebagai berikut.
dy/dx=U'V+UV'
dy=U'Vd(x)+UV'd(x) ... (i)
Jika y diganti dengan UV maka (i) dapat ditulis menjadi:
d(UV)=U'Vd(x)+UV'd(x) ... (ii)
U'(x)dx=dU dan V'(x)dx=dV
(ii) dapat ditulis menjadi:
d(UV)=VdU+UdV ... (iii)
Persamaan (iii) dapat juga ditulis menjadi:
UdV=d(UV)-VdU ... (iv)
Dengan mengintegralkan kedua ruas pada persamaan (iv) maka akan diperoleh rumus sebagai berikut:
∫UdV=∫d(UV)-∫VdU
⇔∫UdV=UV-∫VdU
Rumus di atas merupakan rumus integral parsial secara umum.
Untuk menyelesaikan integral dengan integral parsial yang perlu diperhatikan adalah pemilihan U dan dV. Fungsi yang dimisalkan sebagai U adalah fungsi yang kalau diturunkan terus-menerus menghasilkan 0(nol). Sedangkan fungsi yang dimisalkan dengan dV adalah fungsi yang dapat diintegralkan. Untuk lebih jelasnya, perhatikan dua contoh di bawah ini.
Contoh:
∫x√x-7 dx=...
misal U=x ⇔ du=dx
dV=√x-7 dx
⇔ ∫ dV=∫ √x-7 dx
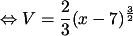
∫x√x-7 dx=∫ UdV=UV-∫ VdU

∫ xcosx dx = ...
misal U=x ⇔ du=dx
dV=cos x dx
∫ dV=∫ cos x dx
V=sin x
∫ xcos x dx=∫ UdV=UV-∫ VdU
∫ xcos x dx=x(sin x)-∫ sin x dx
∫ xcos x dx=xsin x-(-cos x)+C
∫ xcos x dx=xsin x+cos x+C
Tanda bahwa penyelesaian integral parsial sudah selesai adalah tidak terdapat lagi bentuk integral. Jika masih terdapat bentuk integral berarti prosesnya belum selesai. Pada kasus tertentu, penyelesaian integral dengan teknik integral parsial tidak cukup sekali. Contoh di bawah ini, penyelesaian integral parsial perlu dilakukan tiga kali.
∫ x3sin x dx
Untunya ada alternatif yang lebih mudah, yaitu dengan metode Tanjalin.
Proses awalnya sama dengan proses yang telah dijelaskan di atas yaitu membagi integran menjadi dua bagian yaitu U dan dV. Langkah selanjutnya adalah menyajikan U dan dV pada tabel seperti di bawah ini.
| Tanda | Turunkan | Integralkan |
| + | U | dV |
| - | U' | ∫ dV |
| tanda +/- selang-seling | Terus turunkan U sampai hasilnya 0 | Terus integralkan sampai sebaris dengan hasil turunan kesekian U sama dengan 0 |
| baris terakhir | 0 | Integral kesekian dari dV |
Langkah terakhir adalah mengalikan baris ke-1 di kolom U dengan baris ke-2 di kolom dV Tandanya +. Jumlahkan dengan hasil kali baris ke-2 kolom U dan baris ke-3 kolom dV, tandanya -. Dan seterusnya sampai baris terakhir. Untuk lebih jelasnya, perhatikan contoh berikut.
Kita selesaikan soal
∫ x3sin x dx
Misal U=x3 (Karena kalau diturunkan terus-menerus menghasilkan 0)
dV=sin x dx (Bisa diintegralkan)
| Tanda | Turunkan | Integralkan |
| + | x3 | sin x dx |
| - | 3x2 | -cos x |
| + | 6x | -sin x |
| - | 6 | cos x |
| Baris Terakhir | 0 | sin x |
Jumlahkan hasil kali fungsi baris ke-n pada kolom kedua dengan fungsi baris ke-(n+1) pada kolom ketiga, tanda pada kolom pertama juga diikutsertakan. Saya sajikan fungsi-fungsi yang dikalikan menjadi satu warna. Jumlahkan hasil kali fungsi-fungsi yang sewarna (termasuk tandanya juga).
Berikut hasil akhirnya.
∫x3sin x dx
=x3(-cos x)+(-)3x2(-sin x)+6xcos x+(-)6sin x+C
=-x3cos x+3x2sin x+6xcos x-6sin x+C
=(3x2-6)sin x+(-x3+6x)cos x+C
Sekian pembahasan teknik integral parsial semoga membantu Kamu memahami konsep ini.
 Oleh Opan
Oleh Opan
Dibuat 29/04/2011
Seorang guru matematika yang hobi menulis tiga bahasa, yaitu bahasa indonesia, matematika, dan php. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang dimiliki.
Demi menghargai hak kekayaan intelektual, mohon untuk tidak menyalin sebagian atau seluruh halaman web ini dengan cara apa pun untuk ditampilkan di halaman web lain atau diklaim sebagai karya milik Anda. Tindakan tersebut hanya akan merugikan diri Anda sendiri. Jika membutuhkan halaman ini dengan tujuan untuk digunakan sendiri, silakan unduh atau cetak secara langsung.

