Rumus Fungsi Trigonometri Penjumlahan dan Pengurangan Dua Sudut
Rumus Sinus Penjumlahan dan Pengurangan Dua Sudut
Menemukan Rumus
Perhatikan segitiga ABC di bawah ini:
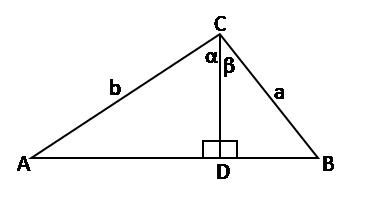
Nyatakan CD, AD, dan BD dalam perbandingan trigonometri untuk sudut α dan β
CD = b cos α = a cos β
AD = b sin α
BD = a sin β
Luas ∆ADC dan Luas ∆BDC
Luas ∆ADC = ½ (AD x CD) = ½ (b sin α x a cos β)
Luas ∆BDC = ½ (BD x CD) = ½ (a sin β x b cos α)
Luas ∆ABC merupakan jumlah dari luas ∆ADC dengan Luas ∆BDC, sehingga
Luas ∆ABC = Luas ∆ADC + Luas ∆BDC
Luas ∆ABC = ½ (b sin α x a cos β) + ½ (a sin β x b cos α)
Luas ∆ABC = ½ (b sin α x a cos β) + ½ (a sin β x b cos α)
Luas ∆ABC = ½ab (sin α cos β) + ½ab (sin β cos α)
Luas ∆ABC = ½ab (sin α cos β + sin β cos α)
Luas ∆ABC menggunakan rumus sinus
Perhatikan gambar di bawah ini:
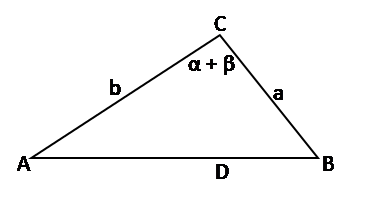
Luas ∆ABC = ½ x a x b x sin (α + β)
½ab (sin α cos β + sin β cos α) = ½ab sin (α + β)
sin α cos β + sin β cos α = sin (α + β)
sin (α + β) = sin α cos β + cos α sin β
Rumus di atas bisa digunakan untuk mendapatkan rumus sin (α - β), dengan cara β diganti -β.
sin (α - β) = sin (α + (-β))
sin (α - β) = sin α cos (-β) + cos α sin (-β)
sin (α - β) = sin α cos β + (- cos α sin β)
[cos (-β) = cos β; sin (-β) = - sin β]
sin (α - β) = sin α cos β - cos α sin β
sin (α - β) = sin α cos β - cos α sin β
Contoh soal dan pembahasan
Soal:
Diketahui tanα-tanβ=1/3 dan cosαcosβ=48/65 (α, β lancip). Nilai sin(α-β)=...
A. 63/65
B. 33/65
C. 26/65
D. 16/48
E. 16/65
Jawaban E

Rumus Cosinus Penjumlahan dan Pengurangan Dua Sudut
Rumus untuk cosinus penjumlahan dan pengurangan dua sudut bisa diperoleh dari rumus sinus penjumlahan dan pengurangan dua sudut yang telah dibahas sebelumnya menggunakan rumus sudut berelasi.
cosα=sin(90°-α)
sinα=cos(90°-α)
Berikut rumus cosinus penjumlahan dua sudut yang diperoleh dengan menggunakan sudut berelasi antara cosinus penjumlahan dua sudut dan sinus penjumlahan dua sudut.
cos(α+β)=sin(90°-(α+β)
cos(α+β)=sin(90°-α-β)
cos(α+β)=sin[(90°-α)-β]
cos(α+β)=sin(90°-α)cosβ-cos(90°-α)sinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
sedangkan rumus untuk pengurangannya
cos(α-β)=cos[α+(-β)]
cos(α-β)=cosαcos(-β)-sinαsin(-β)
cos(α-β)=cosαcosβ-(-sinαsinβ)
cos(α-β)=cosαcosβ+sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
Contoh soal dan pembahasan
Soal:
Jika A-B=60° dan sinAsinB=3/8 maka nilai cos(A+B) adalah...
A. -3/4
B. -1/4
C. 0
D. 1/4
E. 3/4
Jawaban B
cos(A-B)=cosAcosB+sinAsinB
cos60°=cosAcosB+3/8
1/2=cosAcosB+3/8
cosAcosB=1/2-3/8=1/8
cos(A+B)=cosAcosB-sinAsinB
cos(A+B)=1/8-3/8=-2/8=-1/4
Rumus Tangen Penjumlahan dan Pengurangan Dua Sudut
Tangen merupakan perbandingan sinus dan cosinus. Rumus tangen penjumlahan dan pengurangan dua sudut dapat diperoleh dari rumus tersebut. Sebelumnya telah diketahui bahwa rumus sinus dan cosinus untuk penjumlahan (dan pengurangan) dua sudut adalah sebagai berikut.
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
Rumus tangen didapatkan dengan membagi rumus sinus penjumlahan dua sudut dengan rumus cosinus penjumlahan dua sudut di atas.
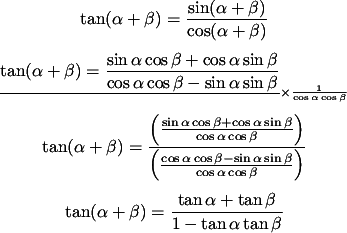
sedangkan rumus tangen pengurangan dua sudut adalah sebagai berikut
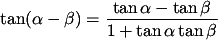
Contoh soal dan pembahasan
Tentukan nilai dari:
a. tan(π/4+y)
b. tan 15°
Jawaban a:

Jawaban b:
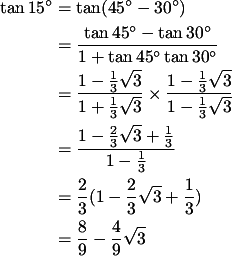
 Oleh Opan
Oleh Opan
Dibuat 06/05/2011
Seorang guru matematika yang hobi menulis tiga bahasa, yaitu bahasa indonesia, matematika, dan php. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang dimiliki.
Demi menghargai hak kekayaan intelektual, mohon untuk tidak menyalin sebagian atau seluruh halaman web ini dengan cara apa pun untuk ditampilkan di halaman web lain atau diklaim sebagai karya milik Anda. Tindakan tersebut hanya akan merugikan diri Anda sendiri. Jika membutuhkan halaman ini dengan tujuan untuk digunakan sendiri, silakan unduh atau cetak secara langsung.

