Konsep Dasar Pemetaan: Pengertian, Sifat, dan Jenis Fungsi
Fungsi adalah sebuah relasi yang memiliki aturan khusus. Fungsi atau pemetaan dari himpunan A ke himpunan B adalah relasi yang memasangkan setiap anggota himpunan A dengan hanya satu anggota himpunan B.
Menurut definisi di atas, sebuah relasi dari himpunan A ke himpunan B dikatakan fungsi jika memenuhi syarat sebagai berikut.
- Setiap anggota himpunan A mempunyai pasangan (tidak jomblo).
- Setiap anggota himpunan A hanya dipasangkan dengan satu anggota himpunan B (tidak selingkuh).
Domain, Kodomain, dan Range
Misal fungsi f memetakan himpunan A ke himpunan B. Himpunan A disebut sebagai domain (daerah asal), himpunan B disebut kodomain (daerah kawan), dan anggota himpunan B yang merupakan peta (pasangan) dari himpunan A disebut range (daerah hasil).
Menyatakan Fungsi
Sebuah fungsi dapat dinyatakan dengan diagram panah, himpunan pasangan berurutan, dan diagram kartesius. Berikut ini adalah contoh fungsi dan bukan fungsi yang disajikan dalam diagram panah.
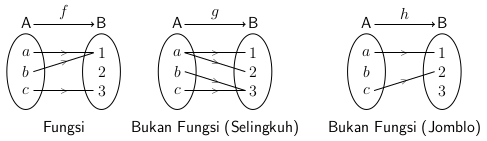
Domain dari fungsi f di atas adalah
A = {a, b, c}
Kodomainnya
B = {1, 2, 3}
dan Range-nya adalah
{1, 3}
Dalam pasangan berurutan, fungsi f dinyatakan sebagai berikut.
{(a,1), (b,1), (c,3)}
Notasi Fungsi
f: A → B artinya f memetakan anggota himpunan A ke himpunan B.
f: a → b atau f(a) = b artinya f memetakan a ke b atau b peta dari a.
f(x) = 2x artinya f memetakan setiap anggota domain ke anggota kodomain dengan aturan peta pada kodomain adalah 2 kali dari setiap anggota domain.
Contoh
Diketahui A = {-2, -1, 0, 1, 2} dan B = {0, 1, 2, 3, 4}. Fungsi f memetakan setiap anggota himpunan A ke himpunan B dengan rumus f(x) = x2. Tuliskan fungsi f dalam himpunan pasangan berurutan dan tentukan range dari fungsi f.
f={(-2,4), (-1,1), (0,0), (1,1), (2,4)}
Rf={0, 1, 4}
Sifat-Sifat Fungsi
Fungsi Into
Fungsi f: A → B disebut fungsi into jika ada anggota himpunan B yang tidak memiliki prapeta (pasangan) dari anggota himpunan A.
Fungsi Injektif
Fungsi f: A → B disebut fungsi injektif jika setiap anggota himpunan B hanya memiliki satu pasangan dengan anggota himpunan A.
Fungsi Surjektif
Fungsi f: A → B disebut fungsi surjektif jika setiap anggota himpunan B merupakan pasangan dari anggota himpunan A. Dengan kata lain, setiap anggota himpunan B atau kodomain merupakan range.
Fungsi Bijektif
Fungsi f: A → B disebut fungsi bijektif jika fungsi f merupakan fungsi injektif sekaligus fungsi surjektif. Artinya, setiap anggota himpunan B mempunyai pasangan dari anggota himpunan A dan masing-masing anggotanya hanya memiliki satu pasangan.
Misalkan terdapat relasi dari himpunan A ke himpunan B. Untuk menentukan apakah relasi tersebut merupakan fungsi atau bukan adalah dengan cara memperhatikan himpunan A. Sedangkan untuk menentukan sifat-sifat sebuah fungsi adalah dengan cara memperhatikan himpunan B.
Diketahui A = {1, 2, 3, 4, 5}, B = {2, 3, 4, 5, 6}, dan C = {2, 4, 6, 8}. Tentukan sifat dari fungsi dalam bentuk himpunan pasangan berurutan berikut.
| Fungsi | Sifat |
|---|---|
| f: C → A dengan f = {(2,1), (4,2), (6,4), (8,5)} | Fungsi Injektif |
| f: A → C dengan f = {(1,2), (2,4), (3,4), (4,6), (5,8)} | Fungsi Surjektif |
| f: C → B dengan f = {(2,2), (4,3), (6,3), (8,5)} | Fungsi Into |
| f: A → B dengan f = {(1,2), (2,3), (3,4), (4,5), (5,6)} | Fungsi Bijektif |
Jenis-Jenis Fungsi
Secara garis besar, fungsi terdiri dari fungsi aljabar dan fungsi transenden. Fungsi aljabar adalah fungsi yang mengandung bentuk aljabar. Sedangkan fungsi yang tidak mengandung bentuk aljabar dinamakan fungsi transenden. Contoh fungsi aljabar adalah fungsi konstan, fungsi identitas, fungsi linear, fungsi kuadrat, fungsi polinom, fungsi modulus, dan sebagainya. Sedangkan fungsi transenden contohnya adalah fungsi eksponen, fungsi logaritma, fungsi trigonometri, dan sebagainya.
Fungsi Konstan
Fungsi konstan adalah fungsi yang berbentuk f(x) = k dengan k adalah sebuah konstanta atau skalar. Berapa pun nilai x disubstitusi, nilainya selalu sama/konstan, yaitu k. Grafik dari fungsi ini berupa garis mendatar sejajar sumbu X.
Fungsi Identitas
Fungsi identitas adalah fungsi memetekan setiap anggota ke dirinya sendiri. Secara umum, fungsi identitas ditulis sebagai f(x) = x. Grafik dari fungsi identitas adalah garis yang membentuk sudut 45° terhadap sumbu X.
Fungsi Linear
Fungsi linear adalah fungsi yang berbentuk f(x) = ax + b dengan a ≠ 0. Grafik fungsi linear berupa garis.
Fungsi Kuadrat
Fungsi kuadrat adalah fungsi yang berbentuk f(x) = ax2 + bx +c dengan koefisien x2, yaitu a ≠ 0. Grafik fungsi kuadrat berbentuk kurva parabola.
Fungsi Polinom
Fungsi polinom adalah bentuk umum dari fungsi konstan, fungsi identitas, fungsi linear, dan fungsi kuadrat. Bentuk umumnya adalah sebagai berikut.
f(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0
dengan an, an-1, ..., a2, a1, a0 bil. real, an ≠ 0, dan a0 konstanta.
Fungsi Irasional
Fungsi irasional adalah fungsi yang berbentuk akar. Contohnya f(x) = √x+1. Fungsi irasional terdefinisi jika bilangan di dalam akar tak negatif (positif atau nol).
Fungsi Pecahan
Fungsi pecahan adalah fungsi yang berbentuk pecahan.
| Misalnya f(x) = | 2x-3 |
| 4x+5 |
Fungsi pecahan terdefinisi jika bilangan pada penyebut pecahan tidak sama dengan nol.
Fungsi Ganjil
Fungsi ganjil adalah fungsi yang memenuhi f(-x) = -f(x). Grafiknya simetris terhadap titik pusat O(0,0). Contohnya adalah f(x) = x3.
f(-x) = (-x)3 = -x3 = -f(x)
Fungsi Genap
Fungsi genap adalah fungsi yang memenuhi f(-x) = f(x). Grafiknya simetris terhadap sumbu Y. Contohnya f(x) = x2 - 9.
f(-x) = (-x)2 - 9 = x2 - 9 = f(x)
 Oleh Opan
Oleh Opan
Dibuat 10/05/2017
Seorang guru matematika yang hobi menulis tiga bahasa, yaitu bahasa indonesia, matematika, dan php. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang dimiliki.
Demi menghargai hak kekayaan intelektual, mohon untuk tidak menyalin sebagian atau seluruh halaman web ini dengan cara apa pun untuk ditampilkan di halaman web lain atau diklaim sebagai karya milik Anda. Tindakan tersebut hanya akan merugikan diri Anda sendiri. Jika membutuhkan halaman ini dengan tujuan untuk digunakan sendiri, silakan unduh atau cetak secara langsung.

