Soal Penggunaan Turunan
Soal 1
Diketahui h adalah garis singgung kurva y=x3-4x2+2x-3 pada titik (1,-4). Titik potong garis h dengan sumbu X adalah
A. (-3,0)
B. (-2,0)
C. (-1,0)
D. (-1/3,0)
E. (1/3,0)
Jawaban D
y=f(x)=x3-4x2+2x-3
f'(x)=3x2-8x+2
titik singgung (1,-4)
m=f'(1)=3(1)2-8(1)+2=-3
Pers. garis singgungnya
y-b=m(x-a)
y-(-4)=-3(x-1)
Titik potong dengan sumbu X (y=0)
0-(-4)=-3(x-1)
4=-3x+3
-3x=1
x=-1/3
Jadi, titik potongnya adalah (-1/3,0)" />
Soal 2
Jumlah dua bilangan positif x dan y adalah 18. Nilai maksimum x.y adalah...
A. 100
B. 81
C. 80
D. 77
E. 72
Jawaban B
Misalkan xy adalah fungsi f.
Jadikan y sebagai peubah x. Karena x+y=18 maka y=18-x.
f(x)=xy=x(18-x)=18x-x2.
Nilai maksimum diperoleh jika f'(x)=18-2x=0.
Diperoleh -2x=-18; x=9.
Substitusi x=9 ke fungsi f(x).
f(9)=18(9)-92.
Soal 3
Jika y adalah jarak yang ditempuh dalam waktu t
y=t3+t2-t+1
maka kecepatan 15m/s akan ditempuh pada saat t=...
Jawaban:
Fungsi kecepatan merupakan turunan dari fungsi jarak
v=y'
v=3t^2+2t-1
Waktu (t) ketika kecepatan 15m/s
15=3t2+2t-1
3t^2+2t-16=0
(3t+8)(t-2)=0
t=-3/8 atau t=2
tidak mungkin t=-3/8 (waktu tidak mungkin negatif)
Jadi kecepatan 15m/s dicapai ketika t=2s
Soal 4
Tentukan nilai dari
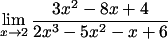
Jawaban:
Kita coba substitusi x=2 ke fungsi

Ternyata kita memperoleh bentuk tak tentu. Secara umum, limit tersebut bisa diselesaikan dengan memfaktorkan pembilang dan penyebut. Selain itu, soal ini bisa juga kita selesaikan menggunakan dalil L'Hopital sebagai berikut.
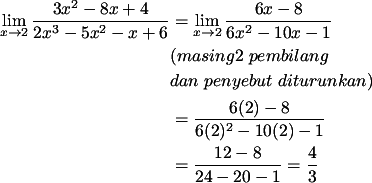
Tulisan ini terkait dengan tulisan pada kategori Latihan Soal.
 Oleh Opan
Oleh Opan
Dibuat 02/06/2014
Seorang guru matematika yang hobi menulis tiga bahasa, yaitu bahasa indonesia, matematika, dan php. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang dimiliki.
Demi menghargai hak kekayaan intelektual, mohon untuk tidak menyalin sebagian atau seluruh halaman web ini dengan cara apa pun untuk ditampilkan di halaman web lain atau diklaim sebagai karya milik Anda. Tindakan tersebut hanya akan merugikan diri Anda sendiri. Jika membutuhkan halaman ini dengan tujuan untuk digunakan sendiri, silakan unduh atau cetak secara langsung.

