Rumus-Rumus Logaritma

Lagi-lagi rumus. Selalu always matematika itu identik dengan rumus tidak pernah never bab matematika gak ada rumusnya. Kita jadikan saja rumus itu sebagai alat dan bahan untuk menyelesaikan masalah/problem/soal. Dengan begitu, rumus akan terlihat kegunaannya. Jangan langsung berpikir kalau rumus itu melulu harus dihapalkan. Selain hapal, perlu juga memahami bagaimana menerapkan rumus tersebut pada soal. Begitu pun dengan rumus yang akan kita pelajari kali ini, terlihat seperti sebuah aturan yang banyak dan membosankan. Tapi tenang saja, dengan sering-sering latihan lama-kelamaan akan terbiasa dengan rumus-rumus tersebut. Mari kita perhatikan terlebih dahulu rumus-rumus logaritma.

Latihan soal
2⁶log 16-3.⁶log 4+⁶log 9=...
Penyelesaian

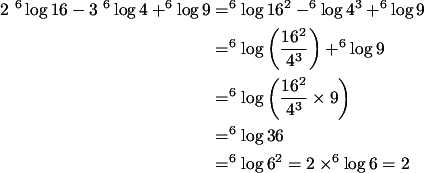
²log 25×⁵log 3×⁹log 32=...
Penyelesaian

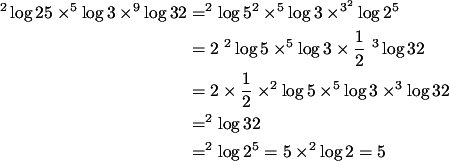
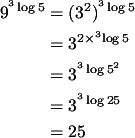
Jika log 2=p dan log3=q maka log(9/4)=...
Penyelesaian

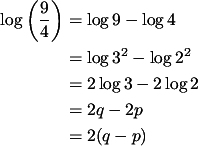
Jika ³log 2=m dan ²log 7=n maka ¹⁴log 54=...
Penyelesaian

Pembuktian Rumus Logaritma

Rumus logaritma perkalian
Logaritma perkalian dua bilangan sama dengan jumlah logaritma dari masing-masing bilangan.
^alog (b×c)=^alog b+^alog c

Bukti:
Misal ^alog b=x maka a^x=b
^alog c=y maka a^y=c

b×c=a^x×a^y

dengan menggunakan aturan pangkat, diperoleh
b×c=a^x+y
menurut definisi logaritma bentuk terakhir menjadi
^alog (b×c)=x+y
ganti x dan y dengan pemisalan awal
^alog(b×c)=^alog b+^alog c

Rumus logaritma pembagian
Logaritma pembagian dua bilangan sama dengan pengurangan logaritma dari pembilang numerus oleh penyebut numerus.

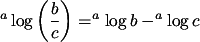
Bukti:
Misal ^alog b=x maka a^x=b
^alog c=y maka a^y=c

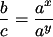
dengan menggunakan aturan pangkat, diperoleh

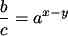
menurut definisi logaritma bentuk terakhir menjadi

ganti x dan y dengan pemisalan awal

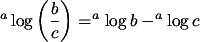
Rumus logaritma bilangan berpangkat
Logaritma dengan numerus berupa bilangan berpangkat sama dengan pangkat dikalikan dengan logaritma bilangan tersebut, ditulis:

^alog bⁿ=n×^alog b

Bukti:
^alog bⁿ=^alog(b×b×b×b×...×) [sebanyak n faktor]
^alog bⁿ=^alog b+^alog b+^alog b+...+^alog b [sebanyak n faktor]
^alog bⁿ=n×^alog b

Mengubah bilangan pokok (basis) logaritma
Bentuk logaritma ^alog b bisa diubah ke dalam dua bentuk berikut:

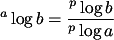
Jika p=b bentuk di atas menjadi:

Bukti:
misal ^alog b=x ⇔ b=a^x

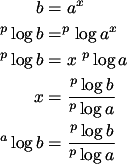
Pembuktian rumus logaritma lainnya
Dari rumus:
^alog bⁿ=n×^alog b
dan

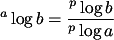
Dapat diperoleh rumus berikut:

Pembuktiannya silakan sebagai latihan.