Latihan Soal SBMPTN
Soal 1
Diberikan matriks sebagai berikut
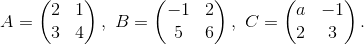
Jika determinan dari matriks 2A-B+3C adalah 10, maka nilai a adalah...
Jawaban
|2A-B+3C|=10
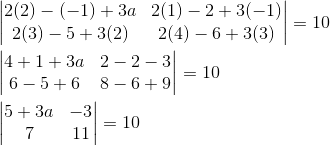
(5+3a)(11)-(-3)(7)=10
55+33a+21=10
33a=10-76=-66
a=-2
Soal 2
Parabola y=2x2-16x+24 memotong sumbu Y di titik A. Jika garis singgung di titik A pada parabola memotong sumbu X di titik (a,0), maka a=...
Jawaban:
Titik potong parabola y dengan sumbu Y diperoleh ketika x=0.
y=24
Berarti titik singgungnya (0,24)
Gradiennya diperoleh dari turunan pertama.
y'=4x-16
m=4(0)-16=-16
Persamaan garis singgungnya
y-24=-16(x-0)
y-24=-16x
garis ini memotong sumbu X di titik (a,0) berarti
0-24=-16(a)
a=24/16=3/2=1 1/2
Soal 3
Nilai maksimum dari F=6x-10y yang memenuhi x+y<=10; x+2y<=10; x>=2; y>=0 adalah...
Jawaban:
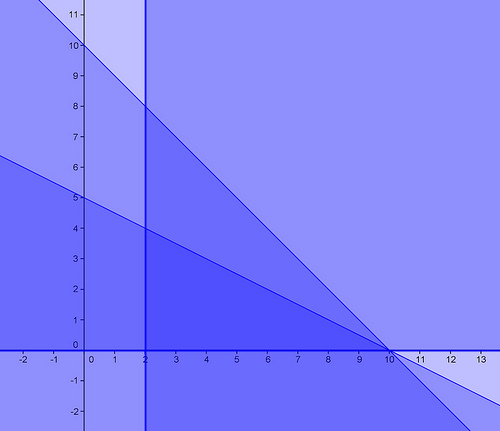
Diperoleh titik pojok (2,0), (10,0), dan (2,4).
Substitusi titik-titik pojok tersebut ke fungsi objektif F.
F(2,0)=6(2)-10(0)=12
F(10,0)=6(10)-10(0)=60
F(2,4)=6(2)-10(4)=12-40=-28
Nilai maksimumnya adalah 60.
Soal 4
Jika g(x-2)=2x-3 dan (fog)(x-2)=4x2-8x+3 maka f(-3)=...
Jawaban:
(fog)(x-2)=f(g(x-2))=4x2-8x+3
f(2x-3)=4x2-8x+3
Misalkan 2x-3=-3; 2x=0; x=0
f(-3)=0-0+3=3
Soal 5
Nilai rata-rata ujian matematika dari 39 siswa adalah 45. Jika nilai Joni digabung dengan kelompok itu, maka nilai rata-ratanya menjadi 45,5. Nilai Joni adalah...
Jawaban:
Gunakan rumus rata-rata gabungan.
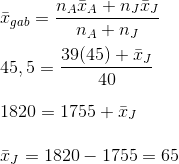
Soal 6
Jika 2log x+4log√y=4log z2, maka z2=...
Jawaban:
4logx2+4log√y=4logz2
4log(x2√y)=4logz2
z2=x2sqrt√y
Soal 7
Jika p < -3 dan q > 5 maka nilai q-p
A. Lebih besar daripada 9
B. Lebih besar daripada 7
C. Lebih kecil daripada 8
D. Lebih kecil daripada 2
E. Lebih kecil daripada -2
Jawaban yang paling tepat adalah (A) lebih besar daripada 9 karena nilai paling kecil dari q adalah 5 dan nilai p paling besar adalah -3.
Soal 8
Seseorang berjalan dengan kecepatan 12 km/jam selama 1 jam pertama. Pada jam kedua kecepatannya berkurang menjadi sepertiganya, demikian juga pada jam berikutnya kecepatannya menjadi sepertiga dari sebelumnya. Jarak terjauh yang dapat ditempuh orang itu selama perjalanan adalah...
Jawaban:
s=v.t
Pada jam pertama jarak yang ditempuh adalah 12km
Pada jam kedua jarak yang ditempuh adalah (1/3)12=4km
Pada jam ketiga jarak yang ditempuh adalah (1/9)12=4/3km
dan seterusnya, polanya mengikuti deret geometri tak terhingga denga suku awal 12 dan rasio 1/3.
Jarak yang ditempuhnya.
S∞=a/(1-r)
=12/[1-(2/3)]
=12/(2/3)
=12(3/2)=18km
Soal 9
Dua buah mobil menempuh jarak 450 km. Kecepatan mobil kedua setiap jamnya 15 km lebih pendek dari waktu perjalanan mobil pertama. Jika waktu perjalanan mobil kedua 1 jam lebih pendek dari waktu perjalanan mobil pertama maka rata-rata kecepatan kedua mobil tersebut adalah...
Jawaban:
s1=s2
v1t1=v2t2
v1t1=(v1+15)(t1-1)
v1t1=(v1+15)(t1-1)
v1t1=v1t1-v1+15t1-15
-v1+15t1-15=0
-v1t1+15t12-15t1=0
-450+15t12-15t1=0
t12-t1-30=0
(t1+5)(t1-6)=0
t1=6; t2=t1-1=5
v1=s/t1=450/6=75
v2=s/t2=450/5=90
Rata-rata kecepatannya (75+90)/2=82,5km/jam
Soal 10
Jika 2 adalah satu-satunya akar persamaan kuadrat
(1/4)x2+bx+a=0 maka nilai a+b=...
Jawaban:
1/4(2)2+b(2)+a=0
2b+a=-1
"satu-satunya akar" berarti memiliki akar kembar maka
D=0
b2-4(1/4)a=0
b2-a=0
b2-(-1-2b)=0
b2+2b+1=0
(b-1)2=0
b=1
a=-3
a+b=-2
Soal 11
Segitiga ABC siku-siku di a. Jika BC=a. AD tegak lurus BC, DE tegak lurus AC, sudut B=Beta maka panjang DE.
Jawaban:
Gambar segitiga yang cocok dengan soal di atas adalah sebagai berikut.
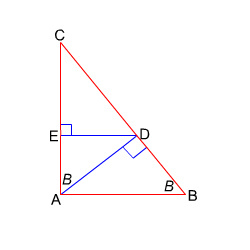
DE = AD sin B
DE = AB sin B sin B
DE = AB sin2B
DE = BC cos B sin2B
DE = a cos B sin2B
Soal 12
Bangun berikut adalah suatu persegi. Jika luas persegi A, persegi B, dan persegi C berturut-turut adalah 16, 36, dan 9 maka luas daerah yang diarsir adalah...
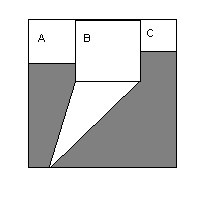
Jawaban:
Luas A=16 berarti sisi A=4
Luas B=36 berarti sisi B=6
Luas C=9 berarti sisi C=3
A+B+C=13 sehingga luas seluruh bangun 13 x 13 = 169
luas arsir=luas seluruh-luas yang warna putih
=169-(luas A+luas B+luas C+luas segitiga)
=169-(16+36+9+(7x6)/2)
=169-(16+36+9+21)
=169-82=87
Soal 13
Misalkan Un menyatakan suku ke-n barisan geometri.
Jika diketahui U5=12
dan log U4 + log U5 - log U6 = log 3 maka nilai U4 adalah...
Jawaban:
logU4+logU5-logU6=log3
log(U4U5/U6)=log3
(ar3ar4)/ar5=3
ar2=3
U4=√U3xU5
=√3x12=6
Soal 14
Penyelesaian pertidaksamaan
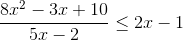
adalah ...
Jawaban
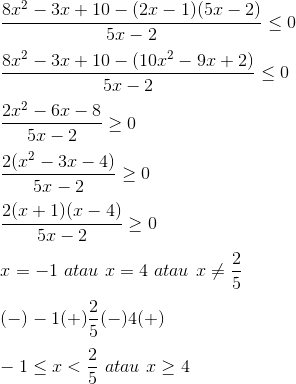
Soal 15
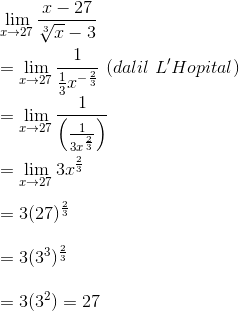 >
>
Soal 16

Jawaban
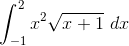
misal u=x+1
x=u-1; dx=du
batas bawahnya u=-1+1=0
batas atasnya u=2+1=3
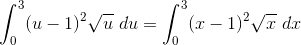
Soal 17
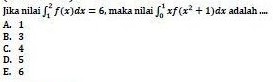
Jawaban
Gunakan metode substitusi pada
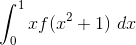
misal u=x2-1
du/dx=2x
dx=du/2x
Batas bawah u=02+1=1
Batas atas u=12+1=2
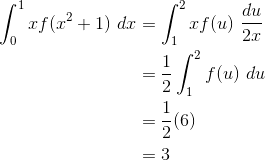
Soal 18

Jawaban
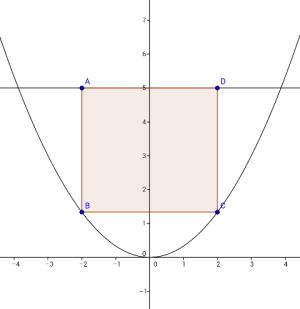
Luas persegi panjangnya adalah sebagai berikut.
L(x)=2(x)(5-(1/3)x2)=10x-(2/3)x3
Luas maksimum diperoleh jika L'(x)=0
10-2x2=0
x2=5
x=akar5 atau -akar5
Luas maksimumnya L=10(akar5)-(2/3)(akar5)3
L=10akar5-(10/3)akar5=(20/3)akar5
Soal 19

Jawaban
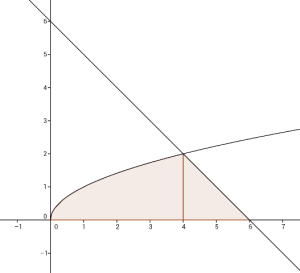
Luasnya
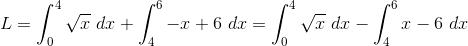
Tulisan ini terkait dengan tulisan pada kategori Latihan Soal.
 Oleh Opan
Oleh Opan
Dibuat 20/12/2013
Seorang guru matematika yang hobi menulis tiga bahasa, yaitu bahasa indonesia, matematika, dan php. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang dimiliki.
Demi menghargai hak kekayaan intelektual, mohon untuk tidak menyalin sebagian atau seluruh halaman web ini dengan cara apa pun untuk ditampilkan di halaman web lain atau diklaim sebagai karya milik Anda. Tindakan tersebut hanya akan merugikan diri Anda sendiri. Jika membutuhkan halaman ini dengan tujuan untuk digunakan sendiri, silakan unduh atau cetak secara langsung.

