Soal Integral Fungsi Trigonometri
Soal Pertama
Soal berikut ini memiliki integran perkalian dua fungsi trigonometri tetapi keduanya tidak bisa diselesaikan secara langsung menggunakan integral substitusi. Oleh karena itu integran diubah terlebih dahulu menggunakan identitas trigonometri, yaitu menguraikan fungsi secan dan contangen ke dalam bentuk sinus dan cosinus.
Setelah disederhanakan, integrannya adalah perkalian cosecan dan cotangen yang bisa diselesaikan secara langsung karena cosecxcotx merupakan turunan dari -cosecx.
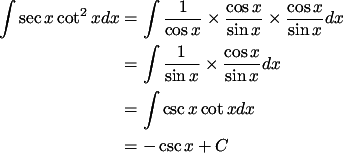
Soal Kedua
Soal di bawah ini memiliki integran fungsi trigonometri berpangkat. Untuk fungsi trigonometri sinus atau cosinus berpangkat dua, bisa diubah terlebih dahulu menggunakan rumus fungsi trigonometri sudut rangkap. Tetapi pada soal ini pangkatnya 4, sehingga perlu diubah dulu berdasarkan identitas trigonometri agar diperoleh fungsi sinus atau cosinus berpangkat dua.
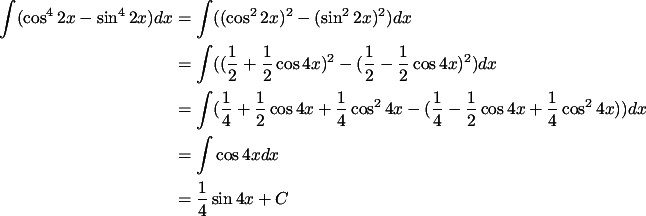
Soal Ketiga
Soal ini memuat integran fungsi trigonometri sinus berpangkat yang berada di posisi sebagai penyebut. Untuk menyelesaikannya kita gunakan identitas bahwa kebalikan dari sinus adalah cosecan, sehingga pangkat dua sinus yang berada di penyebut bisa diubah menjadi fungsi cosecan2. Fungsi cosecan2 ini merupakan turunan dari -cot sehingga integralnya bisa langsung diperoleh.

Soal Keempat
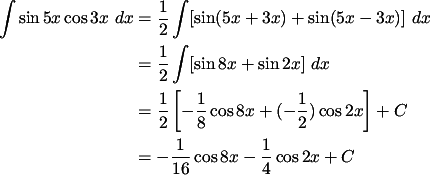
Soal Kelima
Hasil dari ∫(sin2x-cos2x)dx adalah...
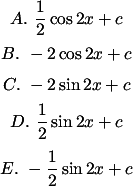
Jawaban D
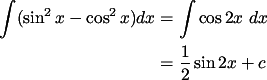
Tulisan ini terkait dengan tulisan pada kategori Latihan Soal, Trigonometri.
 Oleh Opan
Oleh Opan
Dibuat 16/11/2013
Seorang guru matematika yang hobi menulis tiga bahasa, yaitu bahasa indonesia, matematika, dan php. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang dimiliki.
Demi menghargai hak kekayaan intelektual, mohon untuk tidak menyalin sebagian atau seluruh halaman web ini dengan cara apa pun untuk ditampilkan di halaman web lain atau diklaim sebagai karya milik Anda. Tindakan tersebut hanya akan merugikan diri Anda sendiri. Jika membutuhkan halaman ini dengan tujuan untuk digunakan sendiri, silakan unduh atau cetak secara langsung.

